転職活動 2022
昨年12月から今年2月にかけて転職活動をして、4月から新しい会社で働くことになりました。
きっかけ
前職はリブセンスという会社で、主に求人メディアを運営しています。自分は新卒入社から6年間在籍し、データエンジニア/MLOpsエンジニアをしていました。また2018年からは、京都にオフィスを構えて学生アルバイトを受け入れる仕事に取り組んでいました。
京都での仕事は、CS/DSの素養のある学生さんを雇ってMLシステムの効果改善やMLOpsツールの開発を手伝ってもらうというものです。よく誤解されるのですが新卒採用が主眼ではなく、あくまでアルバイトとして学業に支障のない範囲で働いてもらい、会社はその成果を享受し、学生は報酬と就労体験を得る、というのが第一の目的でした。会社からすれば採用というわかりやすい結果を求めがちなところで、よくぞこんな企画を実現させてくれたと思います。設立以来、人事・労務・総務・コーポレートITの方々には本当にお世話になり、大変感謝しています。
この仕事はとても充実したもので、学生時代の自分よりもはるかに優秀なメンバーと接し、多くの刺激を受けました。これほどの人たちを受け入れるからにはしっかり結果を残さねばと思い、試行錯誤を重ねて、少なくとも投資に見合う成果は出せていたはずです。
2020年までに安定的に事業・組織に貢献できる体制が整い、これから拡大というところで、コロナ禍により状況が一変しました。採用活動は全面停止となり、対面でのペアプロやホワイトボードを使うディスカッションもできず、生産性が大きく下がってしまいました。最終的には会社の状況もあいまって、オフィスの閉鎖とアルバイトの受け入れ終了が決まりました。
要はこうして手離れが良くなってしまったのが転職のきっかけです。京都オフィス以前からやっていたML基盤構築の仕事でも会社に十分に貢献できたので、良いタイミングなのでしょう。
12月 会社選び
11月末に上長に退職意向を伝え、年内で候補固め〜年明けから選考〜4月頭に入社というスケジュールを決めました。
12月は多くの知人に話を聞きにいきました。エンジニアの同期や友人はもちろん、前職の上司や人事・PdMの先輩後輩、昔のアルバイト先のはてなでお世話になった人たちなど、十数人ほどでしょうか。この2年はなかなか人と会えなかったので、久々の楽しい時間でした。転職相談のつもりが、いけばなと連珠とサイモン・シンの話で盛り上がって気づいたら3時間、なんてこともありました。
並行してカジュアル面談にも行きました。データに関わる仕事があること・前職とは別の領域の事業会社であること以外、面談先は特にこだわりませんでした。このとき役立ったのがLAPRASというサービスです。以前Scoutyという名前だった頃に会社に遊びに行ったのを思い出し、ステータスを変更してみると、予め自分でリストアップしていた会社の半数ほどからアクションがきて驚きました。どこまで再現性のある体験なのかはわかりませんが、こちらから連絡する手間が省けたのはシンプルにありがたかったです。
これらを経て会社選びの軸が定まりました。まずは現在のスキルが活き、待遇が大きく下がらないこと。次に、前職と異なるデータや問題設定を扱えること。そして、そこにいる人と一緒に働きたいと思えることです。これに沿って面談した中から3社の選考を受けることに決めました。
前職の元同僚からもいくつかお誘いをもらったのですが、せっかく初めての転職活動なので普通に市場に出てみたかったのと、知り合いが多いと甘えてしまいそうだったので、今回は遠慮しました。機会があればぜひ飲みましょう!
1月 選考開始
年明けに3社に応募して選考が開始しました。選考過程は全てリモートでした。各社の選考内容の詳細は書きませんが、どの会社でも一般的な面接と技術課題を伴う面接の両方が設定されました。
多少の準備はしたつもりですが、あとでこうすれば良かったなと思うことはたくさんあります。特に仕事についての質問では、地方オフィスの立ち上げというのがエンジニアには珍しい経験だったこともあって、背景や内容を口頭でもっと簡潔に説明できるようにしておくべきでした。
逆に良かったのは、職務経歴書を3つのエピソードに絞って Google Docs 1ページに収めておいたことです。前職で採用側での面接を何度かやったのですが、職務経歴書の項目が多いと、自分が聞きたい部分と相手の伝えたい部分が噛み合わないことがありました。そのことを踏まえ、自分の場合は思い切って細かいタスクや技術スタックの話を省きました。それが功を奏して、そこから聞かれたと思われる質問には、概ね自分の話したかったことを答えられたと思います。
3社とも選考それ自体が良い体験で、難しい問いが投げかけられることはあっても、不快に思うようなことは一切なく、いずれも最後まで選考を受けました。
2月 内定・オファー・承諾
初の転職だったのと、Web系としては長い6年という在籍期間、加えて現在の待遇がそれなりに良かったこともあり、満足できるオファーが出るかは正直不安でした。しかし結果的には3社とも無事内定をもらい、待遇もすべて前職以上で全く不満はありませんでした。中にはいまの1.5倍の額を提示してくれた会社もあって驚きました。
最後の決定にはかなり悩みましたが、 Ubie のオファーを承諾しました。
前職はすでに色々なものが出来上がり存在している環境だったので、キャリアを自由に選べるうちに、新しく動きの速いところに入ってみたい、というのが理由のひとつです。
そしてもうひとつ。自分はもともと、コンピュータやデータは生活や経済を豊かにするためのものと考えていましたが、 Ubie のプロダクトに触れていると、困っている人を助けるのにも使えるんだなと感じます。どちらが良い仕事だとかいった考えはありませんが、次は後者にも関わってみたくなりました。
そんなわけで4月からは新しい環境です。なんか良いことばかり書いてて、実際前職の仕事の幕切れを除けばつらいことも特にないのですが、泥臭い話とかはいっぱいあるので、またお話しましょう!
IndexedDB でつくる連珠棋譜検索
連珠というゲームをご存知でしょうか?
簡単に言えば五目並べのルールを競技として成立するように整えたもので、次のようなことが定められています。
- 15x15の盤を使う
- 黒 (先手) のみ三三・四四・長連が禁手になり打つことができない
- 上級者向けに、序盤の均衡を保つため着手に制約を設ける開局規定が存在する
昨今の世情により自宅で過ごすことが増えた結果、私はなぜかこのゲームにドハマりしてしまい、こんな記事を書いています。
連珠の序盤事情
連珠は序盤の比重が極めて大きいゲームです。例えば序盤3手までのこの局面、

「花月」と呼ばれる作戦ですが、実は白が4手目をどこに打っても黒が勝てることが解明されている、つまり黒必勝の局面となります。
実際は前述の開局規定のおかげで、上級者の対局では黒がこの作戦を採用しても必勝手順通りに進めることはできません。 しかしその場合も「制約がなければこの局面が黒必勝である」ことを前提としてゲームが進行するため、上位クラスで戦うには必勝局面とその手順についての知識をある程度身につけておく必要があります。
ではこうした知識をどこから得るのか、ですが、連珠は将棋や囲碁などに比べて定石の指導書やオンラインコンテンツがそれほど充実していません。 そこでよく用いられる手段が、ひとつはいわゆるAIを使った研究、もうひとつが実戦例を参考にした研究です。 今回は後者についての話になります。
連珠は国内での競技人口こそ少ないですが、驚くほど国際化と棋譜のデータ化が進んでおり、連珠国際連盟が運営する RenjuNet というサイトで世界中の公式戦の棋譜を閲覧することができます。
The Renju International Federation portal - RenjuNet
このサイト自体は機能が限定的で、任意の序盤局面から実戦例を検索することはできないようです。 その代わりに全棋譜の一括アーカイブをXML形式で提供しており(!)、有志によってアーカイブを検索するための専用ソフトが公開されています。
ただし残念ながら既存のソフトのほとんどは Windows でしか動作しません。 そこで今回、Webブラウザで動作する局面検索機能付き棋譜アーカイブビューワを自分で作ってみました。
ブラウザで数万局の棋譜を検索する
というわけでやっと本題に入ります。ここからはプログラミング寄りの話です。
RenjuNet が提供する棋譜アーカイブは、利用規約上転載や再配布が許可されていません。 よって、棋譜をDBサーバに保存しておいて検索機能をWebサービスとして提供する、といったやり方はできません。 そのため取りうる選択肢は、棋譜アーカイブをユーザ各自が RenjuNet からダウンロードし、それをブラウザで開いて閲覧・検索できるようにする、ということになります。
最新の棋譜アーカイブは7万局超の棋譜を含む20MB程度のXMLデータとなっており、局面を入力するたびに全棋譜との一致判定を行うのは流石にパフォーマンスが気になります。 そこで思いついたのが IndexedDB を使う方法です。
IndexedDB はWeb標準に含まれる技術で、ブラウザ上のストレージにオブジェクトのインデックスを構築することができます。 このインデックスは範囲検索・複合キー検索や multi-value に対応しており、 LocalStorage よりも柔軟な用途に対応できます。 また JavaScript ライブラリではなくWeb標準としてネイティブに実装されているので、高いパフォーマンスが期待できそうです。
今回の「局面から棋譜を検索する」という要件は、局面を符号化したものをキー・棋譜IDをバリューとする multi-value インデックスがあれば実現できるので、 IndexedDB はうってつけの技術といえます。
それでは早速、実際に作ったものを紹介します。

入力した局面に追従して棋譜を検索できているのがわかると思います。 このWebアプリは少し前に「連珠ノート」という名前で私が公開したもので、今回の実装はその一機能として組み込んであり、以下のURLから誰でも使えるようになっています。
機能の利用方法は以下の動画でも解説しています。
なお、今のところ棋譜アーカイブの読み込み処理がSafari系のブラウザで動作しないようです。 XMLのパースに DOMParser を利用しているのですが、 WebKit の DOMParser はサイズの大きいファイルを扱えないのかもしれません。
実装の詳細
検索機能の実装は次のような構成になっています。
コードは全て GitHub で公開しているので、興味があればご覧ください。
GitHub - renju-note/renju-note
以下に主要箇所の簡単な説明を書いておきます。
XMLをパースして棋譜を抽出する
XMLから抽出したデータは、以降の処理で扱いやすくするため一旦そのまま IndexedDB に投入しています。 ここではまだ局面の符号化はしていません。 なお IndexedDB のAPIを直接触るのではなく、 Dexie.js というラッパーを使用しています。
https://github.com/renju-note/renju-note/blob/v2.0.0/src/database/rif.ts#L238-L276
局面を符号化する
黒石・白石を1bitとして盤面を1列につき2個の整数、全部で15x2個の整数で表現し、16進数で文字列化して結合したものを局面符号としています。 今の用途では単なるハッシュ値を局面符号としてもよいのですが、一応局面を再現できる方式をとっています。 また、回転・反転して一致する局面は同一の符号で表現されるよう工夫しています。
https://github.com/renju-note/renju-note/blob/v2.0.0/src/database/encoding.ts
局面符号と棋譜IDをインデックスする
こちらが棋譜検索を実現するためのコアロジックです。 棋譜数x10手分の局面を扱うので、最も計算負荷が高い箇所でもあります。 手元のMacBook(2018モデル)でChromeを使うと7万局のインデックスに2分程度かかりました。
https://github.com/renju-note/renju-note/blob/v2.0.0/src/database/analyzed.ts#L50-L77
局面から棋譜を検索する
上で作成したインデックスを利用して棋譜を検索しているところです。 このメソッドをUIコンポーネントから呼び出して利用しています。 IndexedDB のおかげで1回の検索のレスポンスタイムは1~2秒となっています。
https://github.com/renju-note/renju-note/blob/v2.0.0/src/database/analyzed.ts#L79-L117
おわりに
勢いで作ったWebアプリですが、ありがたいことに海外も含めて多くの連珠家の方々に使っていただいており、今後も開発を継続していこうと思います。
また機能のテストには複数人の高段者の方にご協力いただきました。皆様快く引き受けてくださり、とても感謝しております。今後ともよろしくお願いいたします。
IndexedDB を使ってブラウザ上である程度の規模のデータを検索可能にする方法は、ボードゲーム分野にとどまらず様々な応用ができそうなので、何かの参考になれば幸いです。
2018年の振り返り
仕事では機械学習基盤の整備と古い機械学習システムのリプレースをずっとやっていました。 その中で得た知見を発表する機会にも恵まれ、前年よりアウトプットが増えました。
(2月) Developers Summit 2018
(8月) 機械学習工学研究会 (MLSE) 現場を交えた勉強会 #1
機械学習工学研究会 現場を交えた勉強会 #1 - connpass
(9月) Machine Learning Casual Talks #6
Machine Learning Casual Talks #6 - connpass
また、9月からは京都オフィスに異動となり、関西の勉強会にも参加させてもらいました。 特に学生のときにアルバイトしていたはてなの方々にはとてもお世話になっています。
(10月) Machine Learning Meetup KANSAI ※LT発表
Machine Learning Meetup KANSAI - connpass
会社・個人の技術ブログ等も何件か書きました。
来年は登壇や記事の発表だけでなく、OSS貢献などの直接的なアウトプットも増やしていきたいと思います。
論文紹介: Rank and Relevance in Novelty and Diversity Metrics
秋から京都に会社のオフィスができて異動になり、以前から交流のあった id:syou6162 さんにご報告したところ、京都に拠点のあるIT企業の合同論文輪読会に誘っていただきました。
自分の担当回では推薦システムに関する次の論文を取り上げることにしたので、発表用のノートを兼ねて解説を公開します。
Rank and Relevance in Novelty and Diversity Metrics †
推薦システムにおける Novelty, Diversity
Webサービスを利用していて、以下のような経験をした方は多いのではないでしょうか。
- ECサイトで、すでに購入した商品と似たような商品ばかりがおすすめに表示される
- 転職サイトで、提示されるおすすめ求人が互いに似たようなものばかりになる
使われるアルゴリズムにもよりますが、一般的な推薦システムではすでに評価・選択したのと似たようなアイテムが推薦されたり、推薦されるアイテムが互いに似通ったりしがちです。
しかし推薦システムの目的によっては、似たようなものを提示するのではなく、次のような性質が求められることがあります。
- Novelty (新規性): 今まで見かけたことのない目新しいアイテムを推薦できること
- Diversity (多様性): 互いに特徴が異なる複数のアイテムを一度に推薦できること
本論文では、推薦システムの出力の novelty や diversity についての評価指標を提案しています。 また提案指標を用いることで、各アルゴリズムの特徴を客観的に比較できることを実験で示しています。
用語
以下の解説では次の用語を使います。
- ユーザ: 推薦システムの利用者
- アイテム: 推薦システムがユーザに推薦する個々のもの (商品など)
- ランキング: 一度の推薦でまとめて提示されるアイテムのリスト
- レーティング: ユーザのアイテムに対する評価
- Explicit (明示的) なレーティング: 5段階のスターなど
- Implicit (暗黙的) なレーティング: クリックしたかどうかなど
先行研究と問題点
Novelty, Diversity の改善手法と評価指標
推薦システムの Novelty, Diversity を改善する手法は本論文以前にいくつか提案されています。
Novelty については、Zhou 2010 が協調フィルタリングとグラフのスコア伝播を用いた手法を提案しています。 この研究では評価指標として、ランキング中のアイテムの平均自己情報量 (各アイテムを評価したユーザの割合の対数) を用いています。 また Celma 2008 では、 アイテム間の類似関係によるアイテムの発見されやすさを考慮しています。
Diversity については、Ziegler 2005 が貪欲法により再ランキングを行う手法を提案しています。 また Zhang 2008 ではユーザの選好とアイテム間の類似度に基づく二次最適化問題を解くことで diversity の向上を試みています。 これらの研究では評価指標として、ランキング中のアイテム間相互の距離や非類似度を用いています。
評価における問題点
これらの先行研究について、本論文では次のような問題を指摘しています。
まず novelty, diversity に対する定義がそれぞれ異なっており、それらの関係性についてもあまり議論されていませんでした。 そのため各研究で独自の評価指標が用いられ、手法同士を客観的に比較することが困難でした。
またいくつかの研究では評価指標に次のような欠点がありました。
- Ranking-unawareness: ランキング中のアイテムの順位変化による影響が考慮されていない
- Relevance-unawareness: ユーザにとってのアイテムの関連度 (適合度) が考慮されていない
こういった問題に対して、本論文ではユーザの行動モデルを用いて novelty, diversity とその関係性を定義できると主張しています。 また、この行動モデルを用いて novelty, diversity の評価指標を一般化・定式化することを提案しています。
Discovery, Relevance, Choice に基づくランキング評価指標
Discovery, Relevance, Choice モデル
提案されるユーザ行動モデルは次のようなものです。 まず、次の3つのユーザとアイテムの関係を定義します。
- Discovery (発見): アイテムがユーザに発見される (見られる, 知られる, etc.)
- Relevance (関連): アイテムがユーザと関連する (好まれる, 役立つ, etc.)
- Choice (選択): アイテムがユーザに選択される (クリックされる, 買われる, etc.)
ユーザとアイテムにこれらの関係が成立していることを、二値変数を用いて ,
,
と表します。
またそれらの確率を
,
,
あるいは
,
,
のように表します。
例えばECサイトなら、ユーザにが閲覧した商品は であり、ユーザが欲しいと思う商品は
であり、ユーザが購入した商品は
とである、とみなせます。
ここで簡単のため次が成り立つとします。
- アイテムがユーザに発見されるかどうか (discovery) と関連するかどうか (relevance) は独立である
- ユーザは自分に関連する (
) アイテムを発見する (
) と必ずそれを選択する (
)
- ユーザは自分に関連しない (
) アイテムは選択しない (
)
これにより次の式が成り立ちます。
以降ではこのモデルを根幹として、アイテムの novelty やランキングの novlety, diversity をモデル化します。
ランキング評価指標の一般化
本論文が提案する一般化されたランキング評価指標は次の式で表されます。
がアイテムの novelty であり、後ほど discovery, relevance, choice を用いてモデル化されます。
はコンテキストと呼ばれる変数で、ユーザが発見済みのアイテム集合や、アイテムの人気や普遍性をモデルに組み込むために使われます。
これによりアイテムの novelty がユーザとアイテムの現在までの関係によって変化することをモデル化できます。
アイテムの novelty は によって重み付けされます。
つまり、どれだけ novelty の高いアイテムでも、それがユーザに選択されれる可能性が低ければランキングの評価に寄与しない、という条件をつけることができます。
これにより先行研究に対して指摘されていた rank-unawareness や relevance-unawareness の問題を克服することができます。
アイテムの Novelty
ここからは上述の一般化された評価指標から diversity, novelty を導くため、各項を具体的に定式化していきます。
まず の具体的なモデルとして、次の2種類が提案されます。
Popularity-based Novelty
ひとつは novelty を「ユーザがまだそのアイテムを発見していない可能性」とみなした次のモデルです。
には各アイテムを評価したユーザ数などが用いられます。
観測されたレーティング全体から
を推定する方法は後ほど紹介します。
なお本論文では確率 の代わりに情報量
を使う方法も紹介されますが、実験では省略されるため割愛します。
Distance-based Novelty
もうひとつは novelty を「ユーザが既に発見したアイテムとの距離」とみなした次のモデルです。
は
においてアイテム
が選択された場合にアイテム
が選択される確率であり、
はアイテム
の距離 (または非類似度) です。
には、ユーザがランキングを閲覧する前に発見済みのアイテム集合や、ランキング中で対象アイテムの前に出現したアイテムの集合とします。
特に後者はランキングの diversity の評価指標を導くのに使われます。
ランキングの Novelty, Diversity
上記のモデルにより各アイテムの novelty を定式化できたので、次にこれを用いてランキングの novelty, diversity を定式化します。
Browsing モデル
ランキングを閲覧する際には、ランキング上位のアイテムほど選択されやすく、下位のアイテムは選択されにくくなると考えられます。
これは上記のモデルにおいて、 が
の
中での順位に依存すると考えることでモデル化できます。
ここで、アイテムとユーザの関連度 はコンテキストの影響を受けない (ユーザの過去の行動やランキング中の他のアイテムに左右されない) と仮定すると、次の関係が導かれます。
さらに、ランキング において順位
のアイテム
が発見される確率
が、
についての減少関数
で表されると仮定すると、
は次のように表されます。
以上の仮定を導入したモデルを browsing モデルと呼びます。
Browsingモデルにおける は次のように定式化されます。
実際の としては nDCG で用いられる
などをそのまま使うことができます。
さて、以上によりランキングの novelty, diversity は次のように計算できます。
ランキングの Novelty
ランキングの novelty の算出においては、ユーザがランキングを閲覧する以前に知りうる情報をコンテキストとして考えます。
すなわち には事前に観測されたレーティング等を与えることになります。
Popularity-based novelty を用いたランキングの novelty は次のようになります。 これを論文では expected popularity complement (EPC) と呼んでいます。
Distance-based novelty を用いたランキングの novelty は次のようになります。 これを論文では expected profile distance (EPD) と呼んでいます。
ランキングの Diversity
ランキングの diversity の計算では、対象のランキングそのものの情報をコンテキストとして考えます。
すなわち となります。
ランキングの diversity は次のようになります。 これを論文では Expected Intra-List Diversity (EILD) と呼んでいます。
レーティングによる Discovery, Relevance の推定
以上によりランキングの novelty, diversity を定式化できました。
実際にこれらを計算するためには、観測済みのレーティング等の情報を用いて や
を推定する必要があります。
以下ではレーティングを関数
によって表します。
Discovery の推定
コンテキスト のもとでアイテム
が発見済みである確率
の推定値は次のように求められます。
論文では他のバリエーションについても述べていますが、ここでは割愛します。
Relevance の推定
が explicit なレーティングの場合、そのままでは確率
として扱えないため、
(
は微小な差異を無視するための定数) を用いて次のように変換します。
論文では implicit なレーティングについても述べていますが、ここでは割愛します。
評価実験
本論文では diversity, novelty の向上手法ではなくその評価指標を提案しています。 そのため実験は「評価指標の評価」を行うためのものとなります。 実験では、提案指標を用いることで各種レコメンドアルゴリズムや novelty, diversity アルゴリズムの差異を客観的に捉えることができていることを示しています。
評価に用いられているデータセットは次のとおりです。
- MovieLens 1M: 映画に対する5段階の explicit なレーティング
- Last.fm: 楽曲アーティストに対する implicit なレーティング (視聴ログ)
比較対象の推薦アルゴリズムは次のとおりです。
- MF: Matrix Factorization
- CB: Content-Based Filtering
- UB: User-Based Collaborative Filtering
- AVG: Average Rate
- RND: Random
これらに対して上記の EPC, EPD, EILD をランキング上位50件について計算した結果が次のグラフとなります。
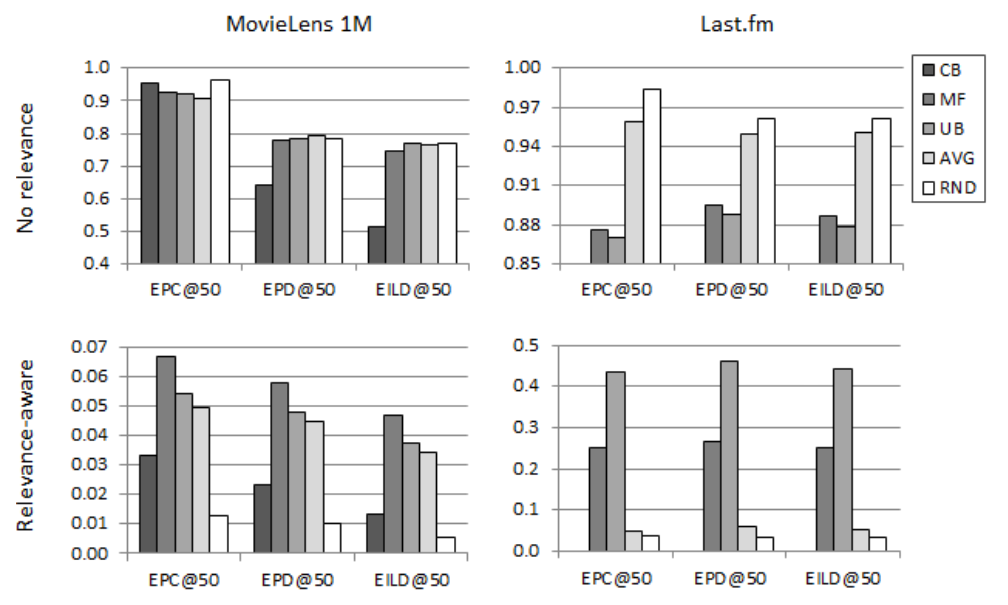
(† Figure 2. より)
Popularity-base vs. Distance-base
まずは popularity-base, distance-base の novelty によって各アルゴリズムがどう特徴づけられるかを見てみます。
グラフの上段は relevance を考慮せずに () 各指標を算出したものです。
ここからコンテンツベースのアルゴリズムとレーティングベースのアルゴリズムの違いが顕著に読み取れます。
Popurality-base のEPCではコンテンツベースのCBがレーティングベースのUB, MFよりもスコアが高いのに対し、Distance-base のEPD, EILDでは逆にCBのスコアが低くなっています。 このことから、提案指標で用いられる popularity-base, distance-base の novelty はそれぞれ各アルゴリズムの特徴を捉えるのに適していると言えそうです。
Relevance-awareness の効果
次に、提案指標により relevance-unawareness の問題に対処できることを示します グラフの下段が relevance を考慮した指標となっており、これを上段と比較するとその効果が見て取れます。
Relevance-unaware な指標ではAVG, RNDが高い novelty, diversity を示していたのに対し、 relevance-aware な指標ではMF, UBがそれらを上回っています。 このことから、 relevance を考慮することで diversity, noveltyが高くともユーザとの関連度が低いアルゴリズムを不当に高く評価しないようにできると言えます。
Relevance-aware な指標では、explicit なレーティングに対してはではMFがUBを上回っており、 implicit なレーティングに対してはそれが逆転しています。 これらは relevance を考慮しない場合は似たような値となっていたので、 relevance を考慮することで diversity, novelty があまり変わらないアルゴリズム同士の優位性を評価できると言えます。
Rank-awareness の効果
最後に、提案手法により rank-unawareness の問題に対処できることを示します。 これを示すには、同じランキングを様々な diversification 手法により再ランキングした結果を比較する必要があります。 実験ではMFの結果を次のような手法で再ランキングした結果を比較対象として取り上げています。
- IA-Select (Vargas 2011)
- MMR (Ziegler 2005)
- NGD (Carbonell 1998)
実験結果は次の表にまとめられています。
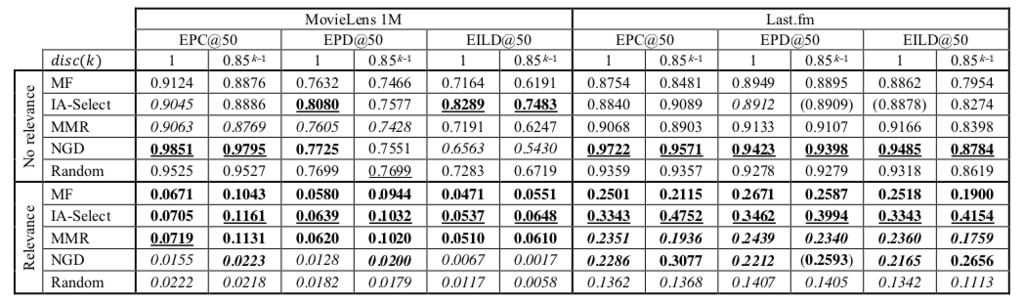
(† Table 5. より)
Relevance を考慮した場合のみについて、いくつか結果を見てみます。 ベースラインとなるMFを上回るスコアを得ている手法はそれほど多くありませんが、IA-Select は全体的にベースラインを上回る結果を残しています。
順位によるディスカウントなしの場合 () とありの場合 (
) を比較すると、IA-Select は MovieLens, Last.fm の両方でスコアを上げていますが、MMR, NGD はスコアを下げていることもあります。
このことから、MMD, NGDでは元のランキングにおいて下位になっている relevance の低いアイテムが上位に浮上している可能性が考えられます。
このように、提案手法を用いることで rank-unaware な指標では発見できなかった各手法の特徴を発見できています。
おわりに
今回は特定の手法ではなく評価指標に関する論文を選んでみました。
検索や推薦などのシステムでは、ユーザがシステム求める性質が様々なので、それぞれの目的に応じて適切な指標を選ぶ必要があります。 本論文で提案される一般化された指標はそういった様々な場面で応用が効きそうです。
またユーザ行動モデルから評価指標を導く一連の考え方は、評価方法を新しく考える必要があるようなケースで参考になりそうです。
機械学習システムの運用課題とコンテナオーケストレーションがもたらすもの
最近仕事では機械学習を使ったアプリケーションをKubernetes上で運用することが多くなっています。 MLOpsのような言葉も次第に浸透してきたりと、システムとしての機械学習をどう運用していくかが活発に議論されるようになってきました。 運用に頭を悩まされてきた身としては心強い限りです。
この記事ではKubernetes(以下k8s)のようなコンテナオーケストレーション技術が、機械学習システム(以下MLシステム)の実行基盤としてなぜ適しているのかについて考えてみました。 注意点として、私はMLアルゴリズムの専門家ではなく、またLinuxやコンテナ技術の専門家でもありません。 あくまで仕事としてMLシステムを運用するためにk8sを利用している立場からの考察です。
TL; DR:
- MLシステムの運用には次のような課題が存在する
- 目的によって求められるワークロードの形態が異なる
- 一時的・断続的に大量の計算リソースを必要とする
- 実環境での試行錯誤に伴ってシステムが変遷する
- コンテナオーケストレーションは次のことを可能にする
- プロセスの実行環境とそのライフサイクルを独立して管理する
- 異なるワークロードを同一のインフラ上でスケジューリングする
→ MLシステムの運用課題はコンテナオーケストレーションによって解決しやすい
機械学習システムの運用課題
1 - アーキテクチャの多様性

MLシステムのアーキテクチャは非常に多様です。 計算としての機械学習は「学習」と「予測」という2つのステップから構成されますが、この2つをどのような形態のワークロードとしてシステムを構成すべきかは目的によって異なります。
最もシンプルなアーキテクチャは、状態を持たない単一のバッチ処理として学習・予測を一気に行うものです。 例えばECサイトで1日1度アイテムをレコメンドするメールマガジンを送信したいといったケースはこの形態で十分と思われます。
ここから一歩進んで、新規データに対してオンラインで予測を行うこともよくあります。 ECサイトの例であれば、新規ユーザに対して登録後すぐにいくつかアイテムを推薦したい、といったケースが考えられます。 オンラインでの予測処理は、リクエストを受けてレスポンスを返すまでの短い時間で計算を完了できることもあれば、リクエストをキューイングしてある程度時間をかけて処理してから改めて結果をプッシュすることもあります。
予測だけでなく学習の一部または全部をオンラインで行う場合も考えられます。 Matrix Factorizationのようなアルゴリズムを用いたレコメンドで、ユーザが新しいアイテムを評価した場合にモデルを再学習するようなケースがこれに当てはまります。
これらに加えて転移学習のような既存のモデルを部分的に更新するような場合まで考えれば、状況はさらに複雑化します。 これ以上は詳しく述べませんが、要するに一つのパターンでは解決できないほどMLシステムのアーキテクチャは多岐にわたるということです。
2 - リソース消費の非連続性
システム形態が多様化しても消費する計算リソースが多くなければ、運用上の問題はそれほど大きくならないかもしれません。 しかしMLシステムは概して通常のシステムより大量の計算リソースを消費します。
機械学習の学習処理は、簡単に言えば大量のデータに複雑なアルゴリズムを適用して有用な関数(モデル)を獲得するという計算です。 処理に必要な計算リソースを肥大化させる要因は、たいていデータとアルゴリズムの両方にあります。 このため計算量を削減することがそもそも困難であり、資金を投入して計算リソースを確保することでしか問題が解決できないこともよくあります。
しかし多くの場合、計算リソースを大量に消費するのは主に学習ステップであり、予測ステップに必要な計算リソースはそれに比べるとずっと少ないのが普通です。 さらに学習は1日や数日に1度、時には数ヶ月に1度行うだけで済むこともあります。 画像認識や自然言語処理など、問題が汎用的であるほどモデル全体の学習の頻度は少なくて済みますが、これは学習によって獲得したモデルが長期に渡って価値を発揮できるためです。
このことはそれ自体MLシステムの長所でもありますが、運用上は悩みの種でもあります。 一定期間に1度しか行われない計算のために常に大量の計算リソースを確保しておくのは大きな無駄となります。 しかし複数のシステムを同一のインフラに同居させようとすれば、マシンのプロビジョニングは複雑化し、システムが採用できる技術の制約は多くなります。
3 - アーキテクチャ・運用レベルの時間的変化
MLシステムの効果は事前に交差検証やバックテストである程度確認できるものの、本質的には実環境で実データを使って運用してみなければ不確実性が大きいものです。 このためMLシステムの開発プロジェクトでは早い段階でシステムを実環境にデプロイし、そこで得られるフィードバックをもとに試行錯誤を繰り返す必要があります。
試行錯誤の過程ではライブラリや収集・利用するデータはもちろん、クラスタリングか次元削減かといった問題設定までもが変わることもあります。 またシステムがある程度の効果を上げるようになれば、学習や予測の頻度を高くしたり、複数のモデルの並行テストやフェイルオーバーが求められることもあります。
これは運用においてシステムの実行環境やリソース要件が頻繁に変更されることを意味します。 変更のたびにマシンの構築やプロビジョニング、キャパシティプランニングが必要となれば当然運用の負担は大きくなります。
さらにMLシステムが価値を発揮するにつれ、ビジネスの売上・利益がそれに強く依存するという状況が生まれることすらあります。 もちろんこれは悪いことではないのですが、システムの可用性が失われればビジネス上の損失が生じることを意味するため、運用には相応の信頼性が求められることになります。
コンテナオーケストレーションがもたらすもの
1 - プロセスの実行環境とライフサイクルの独立化
Linuxにおける計算処理の単位はプロセスです。 コンテナはプロセスを名前空間・ファイルシステム・ネットワークといった実行環境ごとカプセル化したものです。 これを応用すればアプリケーションを依存ライブラリごとイメージとしてアーカイブするといったことも可能になります。
プロセスの実行パターンは成否を表すコードとともに終了するか無限に実行を続けるかの2通りしかありません。 従って高度なシステムでは、複数のプロセスを時にはマシンにまたがって協調動作させることになります。 常に一定数の実行プロセスを維持するサーバや、巨大な計算を並列処理するジョブなどがこれにあたります。
コンテナオーケストレーションの導入により、協調する複数のプロセス(=コンテナ)とそのライフサイクルをひとつのワークロードとして管理できるようになります。 多くのオーケストレーションツールは典型的なワークロードのパターンを予め提供しています。 例えばk8sでは1つ以上のコンテナからなるワークロードの最小の単位をPodとし、常に一定数のPodを実行するようなワークロードにはReplicaSet、加えてPodの世代管理を行うワークロードにはDeploymentといったビルトインのパターンを用意しています。 バッチジョブに適したワークロードパターンとしては、全てのPodを完了まで実行するJob、Jobを定期実行するCronJobなどがあります。
コンテナオーケストレーションの特徴は、プロセスのライフサイクルを実行環境とは独立して管理できる点です。 実行環境が全く異なるプロセスであっても、ライフサイクルが同じであれば同じパターンが適用できます。 これにより従来はミドルウェアやフレームワークが担っていたプロセス管理の役割をオーケストレーションツールに移譲でき、アプリケーションは本来の計算処理とインタフェースの提供に集中できます。
2 - 異なるワークロードの同一インフラ上でのスケジューリング
コンテナオーケストレーションのもうひとつの役割は、コンテナに対するコア・メモリ・ボリュームといったリソースの割当です。 ワークロードが追加されると、オーケストレーションツールは指定されたリソース要件に基づいてクラスタにコンテナ群をスケジューリングします。
このリソース要件の指定とスケジューリングの仕組みもまたプロセスの実行環境とは独立しています。 例えば全く異なるライブラリやフレームワークを用いて実装されたWeb APIサーバとバッチジョブを同一のクラスタ上でスケジューリングすることも可能です。
さらにk8sのようなツールはクラスタを構成する各マシンの負荷状況に応じてワークロードを実行するマシンを選択したり、障害に備えてレプリケーションを分散する機能を備えています。 これらの機能を利用すれば、複数のシステムを効率的に運用しつつ信頼性を保つことができます。
機械学習システムとコンテナオーケストレーションの親和性
ここまでの内容で想像がつくように、先に挙げたMLシステムの運用課題はコンテナオーケストレーションを用いることで解決しやすくなります。
まずワークロード形態の多様性の問題には、オーケストレーションツールが提供する汎用的なパターンを目的に応じて選択することで対処できます。 k8sであればMLシステムに最も適用しやすいのはJobでしょう。 Jobは処理の完了を待つだけでなく、異常終了時のリトライやタイムリミット超過時の強制終了などの機能も持っています。 またReplicaSetやDeploymentはオンラインでの学習・予測を行うサーバを実行するのに役立ちます。 さらにはSparkやTensorFlowのような大規模な分散処理クラスタをk8sのワークロードパターンを用いて構築することも可能です。
次にリソース消費の非連続性の問題には、複数のワークロードを同一インフラ上でスケジューリングすることが有効です。 複数の定期実行されるMLジョブを運用する場合、それらの実行時間をずらしてリソースを共有するといった単純な戦略が考えられます。 あるいはMLシステムと他のアプリケーションを同居させるという選択肢もあります。 ディスクIOやネットワーキングのようなマシン全体のスループットの制限には注意が必要ですが、MLシステムの消費するリソースの大部分はコアやメモリであるため、スケジューリングにおける制約は比較シンプルになります。
最後にアーキテクチャ・運用レベルの時間的変化についても、先の2点と同様のことが言えます。 システムが進化してアーキテクチャが大幅に変わったとしても、新たなインフラを構築せず既存のインフラ上でワークロードパターンを組み換えるという選択肢を取ることができます。 これにより専用のインフラを慎重に設計する時間的猶予が得られたり、成功するかわからないアーキテクチャを一時的に試せるといった利点もあります。 リソース消費の増加に対処したり冗長性を確保するためにはクラスタの拡張が必要ですが、その際のマシンのプロビジョニングが個々のシステムに依存するようなことはなくなります。
これから
MLシステムの重要な運用課題のいくつかはコンテナオーケストレーションにより解決できると思われます。 そしてこの潮流はまさに始まったばかりであり、今後さらなる技術的発展が期待されます。 記事の締めくくりとして、自分がいま気になっている技術をいくつか取り上げたいと思います。
Argo - k8sのCRDとして実装されたワークフローマネージャ
LuigiやAirflowのようなワークフローマネージャをk8sのCustom Resource Definition(CRD)として実現しようというプロジェクトです。 個々のステップがコンテナ化されたジョブを、直列・並列・繰り返しなどを含む柔軟なパターンで記述できます。 CRDはKubernetesのJobやDeploymentのようなワークロードパターンをユーザが定義できる機能です。 Argo UIと呼ばれるUIが提供されているほか、ロードマップでは様々なトリガーへの対応を予定しています。
Seldon - k8s上での汎用MLプラットフォーム
k8s上に汎用的なMLプラットフォームを構築しようというプロジェクトです。 特定のMLライブラリに依存しない汎用的な仕組みのもとでTensorFlowやSparkなどのフレームワークを統一的に運用するという、非常に野心的な取り組みを行っています。 成功するかどうかは未知数ですが、開発は活発に続けられているようです。
RiseML - k8s上での深層学習プラットフォーム
k8s上に深層学習プラットフォームを構築しようというプロジェクトです。 Seldonに似ていますが、こちらは深層学習フレームワークに特化しています。 またコードは公開されているものの、基本的にはPaaSとしてサービスを提供しているようです。
Kubeflow - k8s上でのTensorFlow構築ツール
TensorFlowクラスタとその付随要素をまとめてk8s上に構築しようというプロジェクトです。 TensorFlowのTrainingワークフローをCRDとして実装しているほか、JupyterHubやTensorFlow Servingのような付随するシステムをまとめて立ち上げることができます。 TensorFlowクラスタを自前で運用したい場合には有効かもしれません。
長くなりましたがこのあたりで終わります。