Word Mover's Distance: word2vecの文書間距離への応用

word2vecによって得られる語の分散表現を用いて文書間の距離（非類似度）を計算する手法についての論文を読みました。せっかくなので解説してみます。

[1] Kusner, Matt J., et al. “From word embeddings to document distances.” Proceedings of the 32nd International Conference on Machine Learning (ICML 2015). 2015.

TL;DR

この論文では Word Mover’s Distance(WMD) という文書間距離の計算手法を提案しています。提案手法は手っ取り早く言うと次のようなものです。

文書A, B間の距離 =
A, Bの語同士を対応付けることでAをBに変換するとき、
対応付けのコストが最も低い場合のコストの総和
語xを語yに対応付けるコスト =
x, yの分散表現ベクトルの距離

例えば次の文書 $D_0$ と $D_1$ または $D_2$ との距離を考えてみます。

${ \displaystyle \begin{align} D_0 & \quad \text{The President greets the press in Chicago.} \\ D_1 & \quad \text{Obama speaks to the media in Illinois.} \\ D_2 & \quad \text{The band gave a concert in Japan.} \end{align} }$

ストップワードを除いた上で、各文書の意味の似ている語同士を対応付けます。さらに各対応付けのコストを語同士の分散表現の距離として算出し、その総和を求めます。

下の図は語の対応付けとそのコストを矢印とそれに付与された値で示しています。

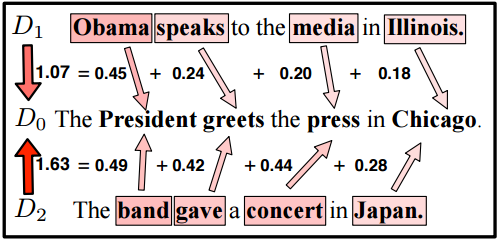
(Figure 2. (Top) from [1])

このコストの総和を文書間の距離と考える、というのがWMDのアイデアとなります。図では $D_0$ に対する距離が $D_1$ のほうが $D_2$ よりも小さくなっています。

論文では文書の近傍を求めるタスクにおいて、多くのデータセットで提案手法により良好な結果が得られたとしています。

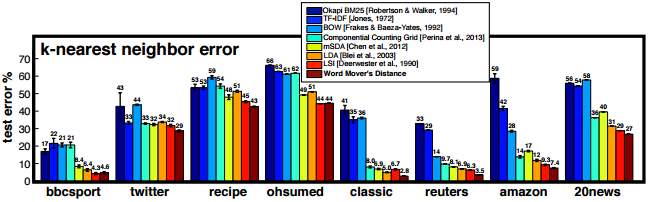
(Figure 3. from [1])

特に twitter のような語数の比較的短い文書からなるデータセットでは、従来手法より良好な結果を残しているようです。

以下では主にWMDの計算アルゴリズムについて、もう少し詳しく解説していきます。

従来の文書類似度計算における課題

単純な文書類似度としては Bag-of-Words (BoW) 表現のコサイン値がよく用いられます。しかし文書同士の共通語が少ない場合、BoWでは文書間の意味的な類似度を測ることが困難です。

例えば上記の文書 $D_0$ , $D_1$ の単純なBoW表現は次のようになりますが、これらは共通語を持たないためベクトル同士のコサイン値はゼロとなります。

${ \displaystyle \newcommand{\sst}[1]{\scriptsize{\text{#1}}} \begin{array}{cccrrrrrrrrc} \ & \ & \ & \sst{chicago} & \sst{greet} & \sst{illinois} & \sst{media} & \sst{obama} & \sst{president} & \sst{press} & \sst{speak} & \\ BOW_0 & = & ( & 1, & 1, & 0, & 0, & 0, & 1, & 1, & 0 & ) \\ BOW_1 & = & ( & 0, & 0, & 1, & 1, & 1, & 0, & 0, & 1 & ) \end{array} }$

従来ではLSIやLDAなどの次元削減手法を利用してこの問題に対処することが試みられていましたが、精度面でそれほど大きな改善を実現するには至っていませんでした。

最近ではニューラルネットの発達に伴い、文書自体の分散表現を計算する手法も提案されています。これらの手法は高い精度を実現できると主張されていますが、NN特有のハイパーパラメータチューニングが必要となる場合もあります。

WMDの考え方

WMDは上記の問題を別のアプローチで解決しようとしています。

上記のとおり文書 $D_0$ , $D_1$ には共通語こそありませんが、人間の目には media と press のようなそれぞれの語同士は非常に近い意味をもつように見えます。 word2vec を用いれば、このような語の意味類似度を捉えた分散表現ベクトルが得られます。

${ \displaystyle \mathbf{x}_w = (x_{w1}, x_{w2}, ... , x_{wn}) }$

WMDではこの性質を利用して文書間の距離を求めます。その考え方は大雑把に言えば、 文書Aの語を類似する（=分散表現間の距離が小さい）語で置き換えて文書Bに変換できるならば、文書A, Bの類似度は大きい（=距離が小さい） というようなものです。

このような考え方に基づいて、WMDでは文書A,B間の距離を、A,Bの語同士を対応付けて文書Aを文書Bに変換するのにかかる「コスト」として計算します。

語の対応付けのコスト

まずある語を別の語に対応付ける場合のコストについて考えます。意味の似ている語同士の対応付けはコストが低い、という特性を満たすよう、語同士の分散表現のL2距離をコストとします。

すなわち、語 $i$ を語 $j$ に対応付けるコスト $c(i, j)$ を次のように定義します。

${ \displaystyle c(i, j) = \lVert \mathbf{x}_i - \mathbf{x}_j \rVert_2 }$

文書の変換コスト

次に、語の対応付けに基づく置き換えにより、ある文書を別の文書に変換することを考えてみます。この置き換えにおいては文書中の意味語（ストップワード以外の語）のみに注目し、語順などは考慮しないものとします。

先程の $D_1$ を $D_2$ に変換する場合、各語を次のように対応付ければよさそうです。

${ \displaystyle \begin{align} \text{obama} & \mapsto \text{president} \\ \text{speak} & \mapsto \text{greet} \\ \text{media} & \mapsto \text{press} \\ \text{illinois} & \mapsto \text{chicago} \end{align} }$

この変換のコストは、単純に考えれば各対応付けのコストの総和とするのが良さそうです。

${ \displaystyle \newcommand{\smt}[1]{\small{\text{#1}}} c(\smt{obama}, \smt{president}) + c(\smt{speak}, \smt{greet}) + c(\smt{media}, \smt{press}) + c(\smt{illinois}, \smt{chicago}) }$

イメージとしては、この総和が小さいほど文書は意味的に類似すると言えそうです。

問題の一般化

これまでの例では意味語の数が同じで、各語も意味的にほぼ１対１に対応づけることができました。しかし次のような文書同士では、単純に語を置換することでは文書を変換できません。

${ \displaystyle \begin{align} D & \quad \text{Obama speaks in Illinois.} \\ D' & \quad \text{The President greets the press in Chicago.} \end{align} }$

任意の２文書間の距離を一貫した基準のもとで計算するには、単純な置き換えによる変換ではなくより一般化された方法を考える必要があります。

そこでまず文書の特徴表現として語の頻度分布を用います。例えば $D$ , $D'$ の特徴ベクトルは次のようになります。

${ \displaystyle \newcommand{\sst}[1]{\scriptsize{\text{#1}}} \begin{array}{cccrrrrrrrc} \ & \ & \ & \sst{chicago} & \sst{greet} & \sst{illinois} & \sst{obama} & \sst{president} & \sst{press} & \sst{speak} & \\ \mathbf{d} & = & ( & 0, & 0, & 1/3, & 1/3, & 0, & 0, & 1/3 & ) \\ \mathbf{d'} & = & ( & 1/4, & 1/4, & 0, & 0, & 1/4, & 1/4, & 0 & ) \end{array} }$

ここでベクトルの各成分は、文書中の語の正規化された出現頻度(TF)となっています。

さらに各語に対応する成分を変換先の文書の複数の語に分配することで、語の頻度分布全体を変換先の分布に移すことを考えます。この変換を次のような行列 $\mathrm{T}$ で表します。

${ \displaystyle \newcommand{\sst}[1]{\scriptsize{\text{#1}}} \mathbf{T} = \left( \begin{array}{cccrrrrrrrc} \ & \sst{chicago} & \sst{greet} & \sst{illinois} & \sst{obama} & \sst{president} & \sst{press} & \sst{speak} \\ \sst{chicago} & 0, & 0, & 0, & 0, & 0, & 0, & 0 \\ \sst{greet} & 0, & 0, & 0, & 0, & 0, & 0, & 0 \\ \sst{illinois} & 1/4, & 0, & 0, & 0, & 0, & 1/12, & 0 \\ \sst{obama} & 0, & 0, & 0, & 0, & 1/4, & 1/12, & 0 \\ \sst{president} & 0, & 0, & 0, & 0, & 0, & 0, & 0 \\ \sst{press} & 0, & 0, & 0, & 0, & 0, & 0, & 0 \\ \sst{speak} & 0, & 1/4, & 0, & 0, & 0, & 1/12, & 0 \end{array} \right) }$

例えばこの行列の7行目は、 $D$ における語 speak の重み1/3のうち、それぞれ1/4と1/12をそれぞれ $D'$ の語 greets と press に移すことを表します。

この対応付全体のコストは、それぞれの語同士の対応コストに分配量に応じた重みかけた値の総和として計算できます。

${ \displaystyle \sum_{i,j} \mathbf{T}_{ij} \, c(i, j) }$

ここで、上の行列はあくまで考えられる変換のひとつでしかありません。 WMDではそのような変換の中でコストの総和が最小となるものを求め、このコストの総和が文書間の距離とします。

最適化問題としての定式化と解法

上記の内容を最適化問題として定式化すると次のようになります。

行列 $\mathbf{T}$ の各行ベクトルは、元の文書中の各語に対応します。その各成分は、元の文書の語分布におけるその語の成分を、変換先の文書の各語にどのように分配するかを表します。よって行の成分の総和は、元の文書の語分布における各語の成分と一致します。

${ \displaystyle \sum_{j} \mathbf{T}_{ij} = d_i }$

同様に行列の各列ベクトルの成分の総和は、変換先の文書の語分布に各語の成分と一致します。

${ \displaystyle \sum_{i} \mathbf{T}_{ij} = d'_j \ }$

コストが最小となる変換のコストを文書間の距離とするので、上式を制約条件とする次の最適化問題を解くことができれば文書間の距離が求まります。

${ \displaystyle \begin{align} \min_{\mathbf{T} \geq 0} & \sum^n_{i,j=1} \mathbf{T}_{ij} \, c(i, j) \\ \text{subject to:} & \sum^n_{j=1} \mathbf{T}_{ij} = d_i \ \forall i \in \{ 1, ..., n \} \\ & \sum^n_{i=1} \mathbf{T}_{ij} = d'_j \ \forall j \in \{ 1, ..., n \} \end{align} }$

実は上の最適化問題は Earth Mover Distance (EMD) と呼ばれる最適化問題の特殊な形式になっています。 EMDを求めるアルゴリズムは既に知られているので、それを用いればWMDを計算できます。

この記事ではEMDについて詳しく解説することはしませんが、以下の記事が詳しいですので興味のある方はご参照ください。

aidiary.hatenablog.com

WMDの長所と短所

WMDの長所としては次のような点が挙げられます。

精度が高い
直感的にわかりやすい
ハイパーパラメータが存在しないためチューニングが不要

逆に短所としては次のような点が挙げられます。

計算量が大きい（類似度計算１回で語数 $p$ に対して [tex: O(p³ \log p)] ）

このような性質から、単なるBoWの類似度では望ましい精度が得られず、かつ計算量が多くても許容できるようなケースでWMDが有効であると考えられます。

なお、ある文書に対する近傍文書を上位k件まで取得できればよいようなケース（文書検索など）では、WMDよりも計算量の小さい下界を利用し、計算量を大幅に抑えることができます。今回はその詳細については割愛しますが、論文には精度の変動の評価も含めて詳しく書かれているので、知りたい方は論文を読まれることをお薦めします。